数据结构 – L1rics的小窝

零散的知识点，一般是容易错的地方，主要的知识点总结在先前的博客中，已经遗失了。

广义表的表头是元素，表尾却是表

KMP算法

void getNext(const char *P, int *next) {
    int i = 1;        // 当前正在计算 next[i]
    int j = 0;        // 前缀末尾位置（前缀长度）
    next[0] = 0;      // 第一个字符没有前后缀
    while (P[i] != '') {
        if (P[i] == P[j]) {
            // 前缀扩展成功
            j++;
            next[i] = j;
            i++;
        } else if (j > 0) {
            // 回退 j，尝试更短的前缀
            j = next[j - 1];
        } else {
            // j == 0，说明无法扩展
            next[i] = 0;
            i++;
        }
    }
}

主要是如何构造对于比较串的next数组，利用了递归的思想，如果新添加的字符不匹配，回退J至先前的前缀

二叉树的性质

在二叉树的第i层上至多有2^i-1个结点
深度为k的二叉树至多有2^k-1个结点
对于任何一棵二叉树，若2度的结点数有n₂个，则叶子数n₀必定为n₂＋1 （即n₀=n₂+1）
具有n个结点的完全二叉树的深度必为[log₂n]＋1
完全二叉树的叶子数l和节点数n满足 l=⌊n/2⌋+1

“线索”指的是把二叉树中原来为空的左、右指针，用来指向在某种遍历顺序下的前驱节点或后继节点。

若某节点左子树为空，则其左指针可改为指向中序前驱。
若某节点右子树为空，则其右指针可改为指向中序后继。

将悬空的指针指向一个头节点头节点的左指针指向root 右指针指向自己。

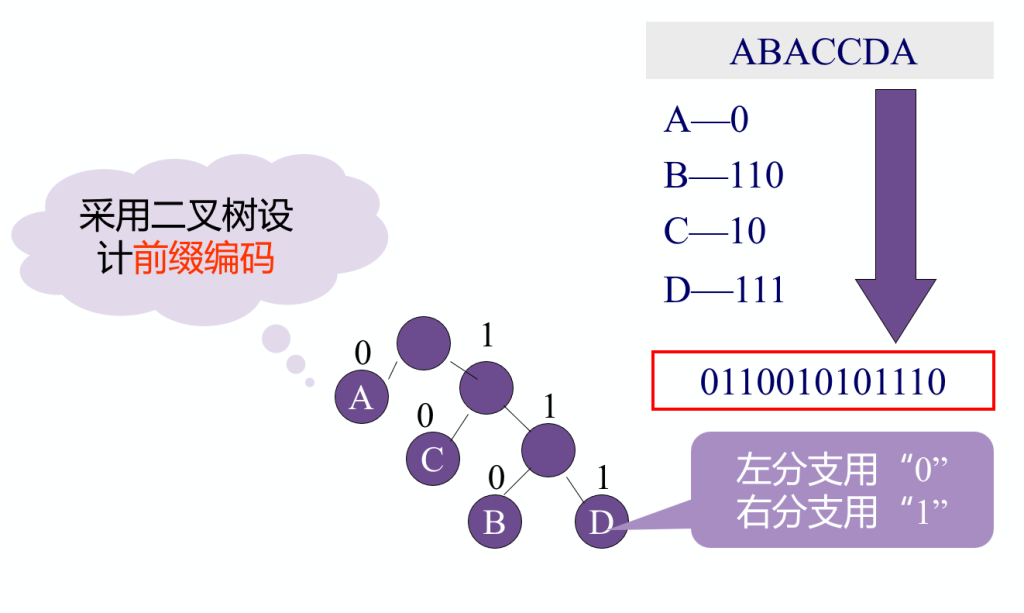
哈夫曼树：采用前缀编码，左分支用“0”，右分支用“1”。

树的存储结构

双亲表示法：每个节点存储其双亲节点的索引（数组中位置）

下标：  0    1    2    3    4
数据：  A    B    C    D    E
父亲： -1    0    0    1    1

孩子表示法：每个节点记录一个链表，链表中是它的所有孩子的编号。

节点 A: → B → C
节点 B: → D → E
节点 C: → ∅

A的孩子为B,C 孩子用链表表示

孩子-兄弟表示法：每个节点只保存第一个孩子和下一个兄弟。

图的定义和术语

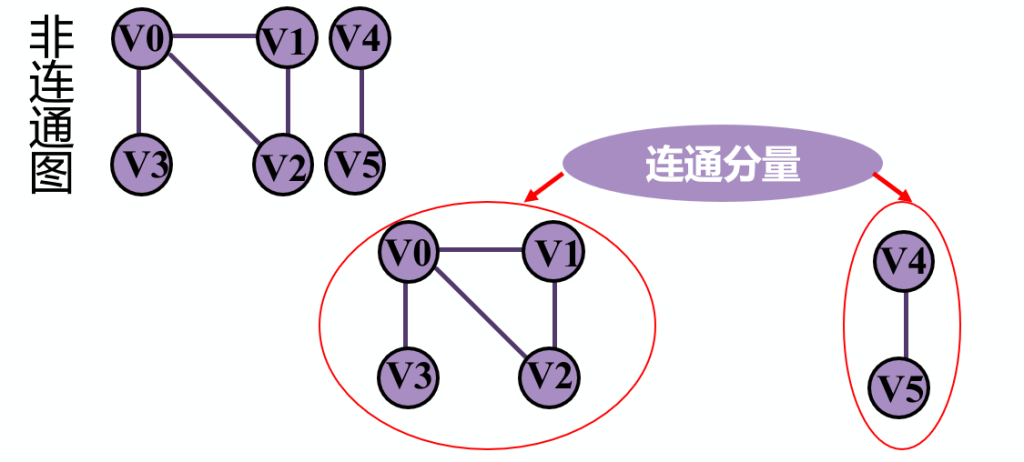
无向图G 的极大连通子图称为G的连通分量。

极大连通子图：该子图是 G 连通子图，将G 的任何不在该子图中的顶点加入，子图不再连通。

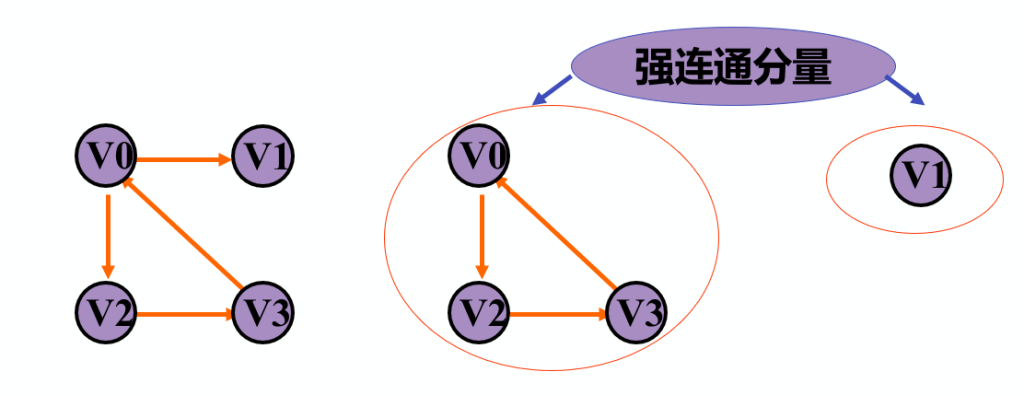
有向图G 的极大强连通子图称为G的强连通分量。

极小连通子图：该子图是G 的连通子图，在该子图中删除任何一条边，子图不再连通。

生成树：包含无向图G 所有顶点的极小连通子图。

生成森林：对非连通图，由各个连通分量的生成树的集合。

图的存储结构

邻接矩阵表示法

邻接表（链式）表示法

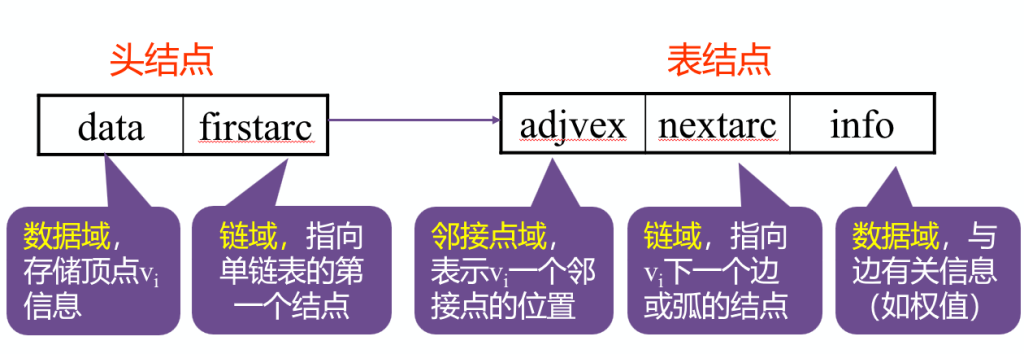
邻接点域：接入点的邻接表的编号

十字链表

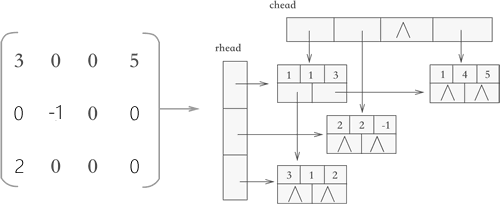
使用十字链表压缩存储稀疏矩阵时，矩阵中的各行各列都各用一各链表存储，与此同时，所有行链表的表头存储到一个数组（rhead），所有列链表的表头存储到另一个数组（chead）中。

下图是十字链表的结构：

普里姆算法（Prim’s Algorithm）（加点）

从任意一个点开始，每次选择权值最小的边，将新节点加入已选集合中，直到所有点都在树中。

详细步骤：

1.选择任意一个点作为起始点（如顶点 0）。

2.标记该点为已访问，并初始化其他点的最小连接边权（dist数组）。

3.重复以下步骤直到所有点都被加入生成树：

找出一个不在树中且与树中某节点连接的最小权值边。
将该边连接的点加入生成树。
更新所有未加入节点的最小连接边权。

克鲁斯卡尔算法（Kruskal’s Algorithm）（加边）

按边权升序排序，逐条选择边，只要不会构成环，就加入最小生成树中，直到包含所有节点。

1.将图中的所有边按权值升序排序；

2.初始化每个顶点为一个单独集合（使用并查集）；

3.从小到大遍历每一条边 (u, v)：

如果 u 和 v 不在同一个集合（即不会成环）：
- 将这条边加入最小生成树；
- 合并 u 和 v 所在的集合；

4.当加入的边数 = 顶点数 – 1 时，停止。

值得注意是，普里姆算法更适合稠密图，克鲁斯卡尔算法更适合稀疏图

迪杰斯特拉（Dijkstra）算法

一顶点到其余各顶点最短路径

先找出从源点v₀到各终点v_k的直达路径（v₀,v_k），即通过一条弧到达的路径。
从这些路径中找出一条长度最短的路径（v₀,u）。
然后对其余各条路径进行适当调整

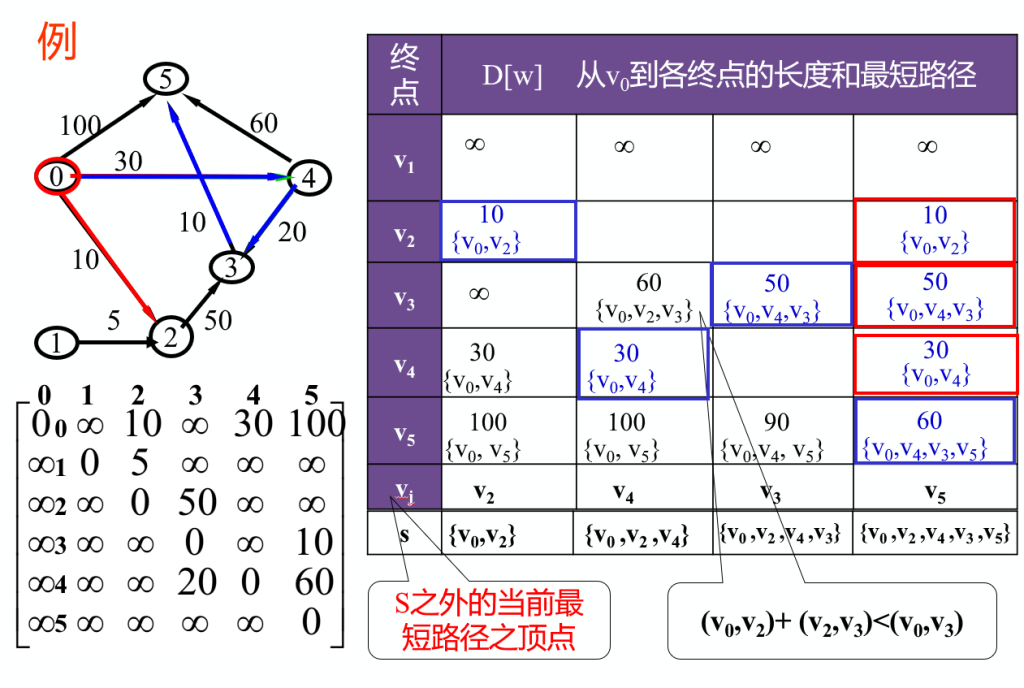
其中比较难理解的是加入新的点后的更新算法，加入的新点为u，那我们就只考虑比较 v0 到 v 的所有路径中，是否 v0 → … → u → v 更短即 dist[v] > dist[u] + graph[u][v] ，每一次我们都只选取距离最小的点，体现了贪心算法的原则为。

// Dijkstra 算法：计算从 start 点出发的最短路径
void dijkstra(int graph[MAXN][MAXN], int n, int start, int dist[], int prev[]) {
    int visited[MAXN] = {0};  // visited[i] = 1 表示点 i 的最短路径已确定

    // 1. 初始化 dist 数组和 prev 数组
    for (int i = 0; i < n; i++) {
        dist[i] = graph[start][i];     // 初始路径长度 = start 直接到 i 的边权
        if (graph[start][i] < INF)
            prev[i] = start;           // 起点能直接到达 i，则前驱是 start
        else
            prev[i] = -1;              // 否则前驱未知
    }
    dist[start] = 0;   // 自己到自己距离为 0
    visited[start] = 1;  // 起点加入集合

    // 2. 进行 n-1 轮处理
    for (int i = 1; i < n; i++) {
        int u = -1;
        int minDist = INF;

        // 2.1 在未访问的点中选择 dist 最小的点 u
        for (int j = 0; j < n; j++) {
            if (!visited[j] && dist[j] < minDist) {
                minDist = dist[j];
                u = j;
            }
        }

        if (u == -1) break;  // 没有可以继续的点，退出
        visited[u] = 1;      // 将 u 加入集合

        // 2.2 用 u 去更新它的邻接点 v
        for (int v = 0; v < n; v++) {
            if (!visited[v] && graph[u][v] < INF) {
                if (dist[v] > dist[u] + graph[u][v]) {
                    dist[v] = dist[u] + graph[u][v]; // 更新最短路径
                    prev[v] = u;                     // 更新路径上的前驱节点
                }
            }
        }
    }
}

弗洛伊德（Floyd）算法

弗洛伊德算法也是路径最短的算法一种，不过是计算计算任意两点间的最短路径。

使用动态规划思想，三重循环尝试用中间点 k 来更新任意点 i 到点 j 的最短距离。

for (k = 1; k <= n; ++k)
    for (i = 1; i <= n; ++i)
        for (j = 1; j <= n; ++j)
            if (dis[i][j] > dis[i][k] + dis[k][j])
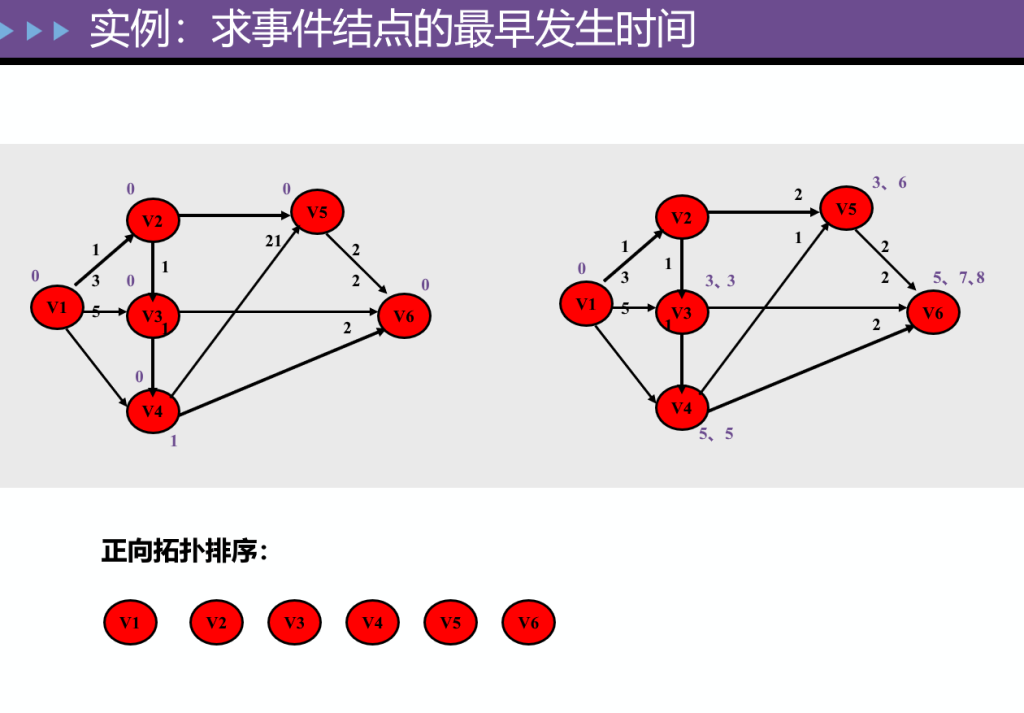
                dis[i][j] = dis[i][k] + dis[k][j];

拓扑排序与关键路径

构造拓扑序列步骤:

从图中选择一个入度为零的点。
输出该顶点，从图中删除此顶点及其所有的出边。

重复上面两步，直到所有顶点都输出，拓扑排序完成，或者图中不存在入度为零的点，此时说明图是有环图，拓扑排序无法完成，陷入死锁。

查找

平均搜索长度ASL：关键字的平均比较次数

ASL总结：

顺序查找：查找成功(n+1)/2，查找失败n+1
折半查找： (log₂n)向下取整 + 1
分块查找：log₂(n/s+1)+s/2 S为每块内部的记录个数，n/s即块的数目
装填因子：表中记录数/表的长度

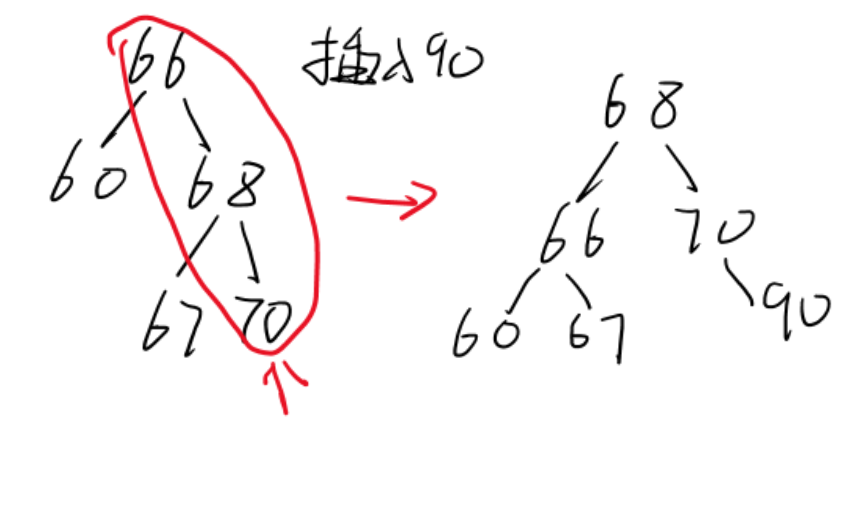
平衡二叉树

失衡的最小子树的根结点a在插入前的平衡因子不为0，且是离插入结点最近的平衡因子不为0的结点的。

平衡方法：

从插入节点从下往上寻找最小的不平衡子树找到根节点
在插入节点到根节点上，画出最邻近的三个路径节点
对这三个节点进行平衡
其余的子树按照左边小，右边大的定义放上去
最后把整理好的数接入子树

排序

插入排序：时间复杂度 n² 空间复杂度 1 稳定
折半插入排序：时间复杂度 n² 空间复杂度 1 稳定平均优于插入排序
希尔排序 :“逐段分割”将相隔某个增量dk的记录组成一个子序列让增量dk逐趟缩短,最后一趟增量为1。时间复杂度 O(n^1.25）～O（1.6n^1.25）—经验公式 // 空间复杂度为 o(1) // 不稳定
快速排序：时间复杂度O( nlog₂n ) //空间复杂度 log₂n（递归要用到栈空间）// 不稳定
基数排序：时间复杂度O(d( n+rd))//空间复杂度O(n+rd)//稳定n个记录每个记录有 d 位关键字关键字取值范围rd(如十进制为10)
堆排序：时间复杂度O(nlog₂n)//空间复杂度O（1）//不稳定

关于快速排序

基本思想：

任取一个元素 (如第一个) 为中心
所有比它小的元素一律前放，比它大的元素一律后放，形成左右两个子表；
对各子表递归快速排序，直到每个子表的元素只剩一个
每一趟的子表的形成是采用从两头向中间，交替式逼近法

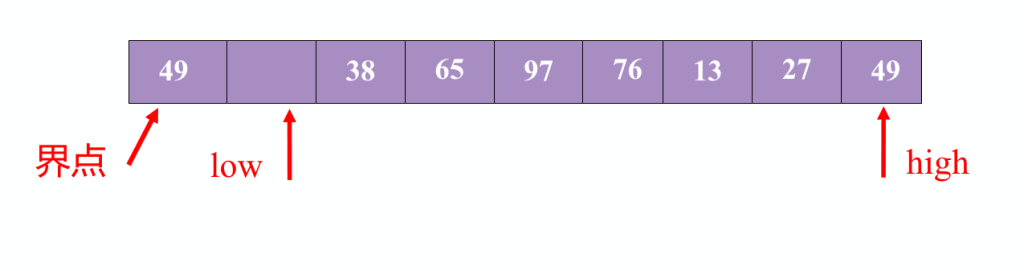
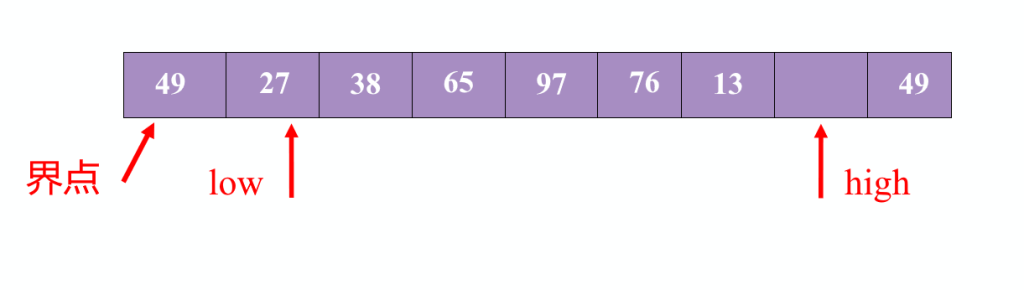
具体操作是通过表头表尾两个指针实现。

与界点相比，如果high指针指向的数据小，就将其数据放在low指针位置，同时low指针开始移动。

直到两个指针相遇，将哨兵数据放入相遇位置。对其左右的子表重新操作。

void QSort ( SqList &L，int low,  int  high ) 
{  if  ( low < high ) 
    {  pivotloc = Partition(L, low, high ) ;
        Qsort (L, low, pivotloc-1) ; 
        Qsort (L, pivotloc+1, high ) 
     }
}

int Partition ( SqList &L，int low,  int  high ) 
{  L.r[0] = L.r[low];   pivotkey = L.r[low].key;
   while  ( low < high ) 
    { while ( low < high && L.r[high].key >= pivotkey )  --high;
                 L.r[low] = L.r[high];
      while ( low < high && L.r[low].key <= pivotkey )  ++low;
                 L.r[high] = L.r[low];
     }
    L.r[low]=L.r[0]; 
    return low;
}

堆排序

堆的建立：自下而上交换形成堆，直到堆顶，然后又自上而下监督，针对交换的元素重新建堆

堆的重新调整：输出堆顶元素后，以堆中最后一个元素替代之。将根结点与左、右子树根结点比较，并与小者交换。重复直至叶子结点，得到新的堆